| TEBER.biz | | Home | Turkish | | |||||||
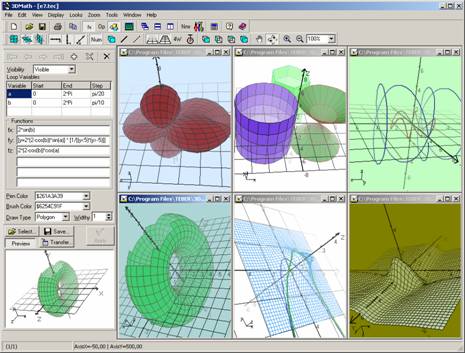
| >> 3DMath Explorer | ||||||||
|
||||||||
|
|
Questions or problems regarding this web site
should be directed to info@teber.biz. Copyright © 2002 Dursun TEBER. All rights reserved. ( http://www.teber.biz ) Last modified: 15/09/2002. |