1. GRAPH SYSTEMS AND MAIN OF DIMENSION

1.3. Dimensions of Objects on the Graph Space

After this information let's turn back article about dimensions of objects on the graph space.

As an enter to the subject, ask yourself 'What is dimension of an simple sphere?' If you are in those people that say ‘it has 3 dimension’. Please continue to read this article.

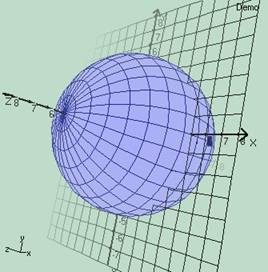
Below you can see mathematical expression of a sphere (curve sphere) that has a center on the origin and has a radius 5.

  0<a<Pi

  0<b<2*Pi

fx(a,b) = 5*sin(a)*cos(b)

fy(a,b) = 5*cos(a)

fz(a,b) = 5*sin(a)*sin(b)

Now let's plot this curve with 3DMath Explorer. If we chose sample periods a and b as pi/15, we get below pictures.

  a(step)=pi/15

  b(step)=pi/15

Maybe after looking these graphs, again you can say these spheres have 3 dimensions. Yes vision of these spheres has 3 dimensions and the curve (curve sphere) can exists in a 3 dimensional coordinate system. But in reality is this curve has 3 dimensions?

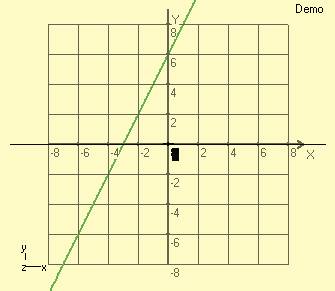
Let's deal with the subject step by step (from simple to more complicated samples - induction). For example let's take a simple function curve. y=2*x+6 is a simple function curve and it exist on a plane called XY plane. If you call above curve (the curve sphere) as a 3 dimensional curve, you may say this curve is 2 dimensional. Vision of simple function curves became 2 dimensional, only if they draw in a 2 dimensional coordinate system. But these curves also can be drawn in 3 dimensional coordinate systems. In this case (when they are drawn in a 3 dimensional coordinate system) their vision become 3 dimensional. Then should we say this curve has 3 dimensions? Could a property of an object (whether it is in an imaginary word or in a reel word) be change from place to place?

Let us make some experiment on this sample curve with 3DMath Explorer before continuing the subject. The y=2*x+6 simple function curve is defined in a 3 dimensional coordinate systems as below.

  -8<x<8

fx(x)= x

fy(x)= 2*x+6

fz(x)= 0

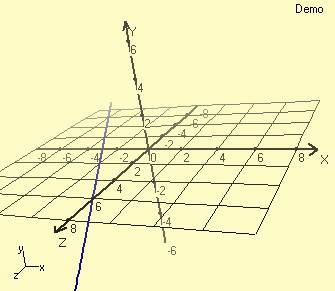
A similar curve that drawn in XZ Plane is curve z =2*x+6 and its 3 dimensional coordinate systems defination is;

  -8<x<8

fx(x)= x

fy(x)= 0

fz(x)= 2*x+6

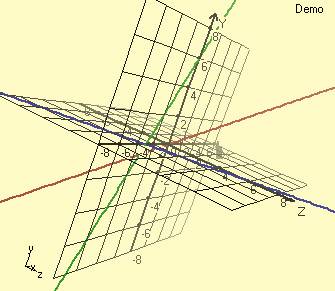
A simple curve equation that has a 45-degree angle to all axis’s may be defined as;

  -8<m<8

fx(m) = m

fy(m) = m

fz(m) = m

Now let’s see all of this curves together on the same screen.

At the same time let’s define XY, XZ and YZ planes that exist in this graph as assistant plot elements. Their mathematical expressions in 3 dimensional coordinate systems are; 

XY plane:   -8<x<8   -8<y<8 fx(x,y) = x fy(x,y) = y fz(x,y) = 0

XY plane:   -8<x<8   -8<z<8 fx(x,y) = x fy(x,y) = 0 fz(x,y) = z

YZ plane:   -8<y<8   -8<z<8 fx(y,z) = 0 fy(y,z) = y fz(y,z) = z

If we turn back the subject, what is the reason of wrong answers for questions about dimension of object in mathematics? As you see, people mix up dimension of objects with dimension of coordinate system they are drawn in.

I hope we bring the problem to light. Now questions that we should ask and try to find answers is ‘How could we define dimension of a curve? Which criteria can we use?’ As you see in above example we cannot define curve dimension with coordinate system that they themselves defined, drawn and exist in. We shouldn’t mix curve dimensions and coordinate system dimensions.

Answer of this questions lies on properties of objects like length, surface area and volume. Objects in math space have or have not these properties with their dimensions.

I think now we should study length, surface area and volume properties. Height of a straight line is its length. A rectangle has two lengths as width (wideness) and height. Rectangle borders a area in a plane and has a surround/circle length. A rectangle prism has three lengths as width (wideness), height (length) and height (depth) properties. A rectangle prism borders a volume in a space and a total surface area with 6 surface that it has.

Now let’s group features (properties) that objects have with their dimensions.

One Dimensional Objects

   • Have a length.

   • If they haven’t got a certain start and stop points (or they have joined start and stop point (or edge)) like circle or rectangle, then we mansion about their having surround/circle length.

   • Haven’t got surface arias and volumes.

   • Couldn’t be exist in real word. They could only be in mind or be vision that projected to (or reflect from) a paper and a computer display.

Two Dimensional Objects

   • Have surface areas.

   • could be mansion about having surround/circle length. (might have surround/circle length)

   • Haven’t got volume.

   • Couldn’t be exist in real word.

Three Dimensional Objects

   • Have volumes.

   • be mansion about having width (wideness), height (length) and height (depth, thickness) properties.

   • Have got a volume.

   • Could be exist in real word.

The last items must be take your attention. The real world is 4 dimensional with time dimension. In this world, objects exist in a 3 dimensional space with a cross-section of dimension time that we call it as ‘now’. To exist in 3 dimensional real world space, a object must have a volume. 1 and 2 dimensional objects couldn’t be existed in real world, as they haven’t got volume.

Henceforth we can make this classification: objects that only have a height as length are 1 dimensional, objects that have surface areas but don’t have volume are 2 dimensional and objects that have volume are 3 dimensional .

After making this classification, if we turn back to the question about dimension of sphere, however this sphere graph is a 3 dimensional graphs as it drawn in a 3 dimensional coordinate system, in fact the sphere is a 2 dimensional object. Because this sphere has a surface area but it do not have a volume.

Now, even when I have been writing this article, I am hearing objections. For example you may say ‘How does a sphere not has a volume? Isn’t there a formula about sphere volume’. Yes, of course there is a volume formula of sphere. But when we mansion about this formula, we also use a statement as ‘volume of a filled sphere’ .

A simple sphere curve borders a volume with its surface area in the space (in math. space). But in fact it is only a cover, a shell. As nothing that doesn’t have a thickness (height, depth) could have a volume and this cure sphere doesn’t have a thickness, it also couldn’t have a volume.

(Here I want to make explanation in parenthesis not to get headache by your possible questions that come to your head letter on: I said before no objects that haven’t volumes could have exist in real world. Now I am saying this 2 dimensional sphere (curve sphere) do not have a volume. So this sphere couldn’t be exist in real world. Then how an object that in reality do not exist could border a volume in the space. Yes, a 2 dimensional object couldn’t exist in real world and as a result of this couldn’t border anything. But when the space in question is the math. space (graph space), 1 and 2 dimensional objects could be exist in this space. In fact they are real in this imaginary world (in math. space). So 1 dimensional objects like circle and rectangle could border an area and 2 dimensional objects like this 2 dimensional sphere could border a volume in this space.)

To add a third dimension to 2 dimensional sphere object above, we must give it thickness (depth) dimension. We can do this by making radius 5 as a variant. 0

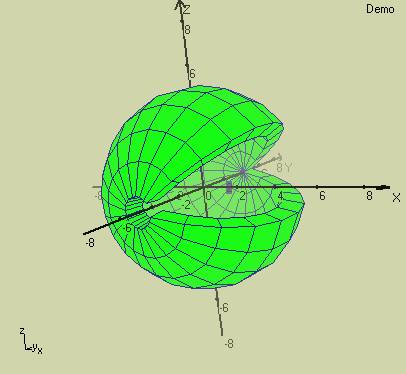
      0<a<Pi    and a(step)=0.3

  Pi/5<b<2*Pi and b(step)=0.3

      4<r<5      and r(step)=1

fx(a,b,r) = r*sin(a)*cos(b)

fy(a,b,r) = r*cos(a)

fz(a,b,r) = r*sin(a)*sin(b)

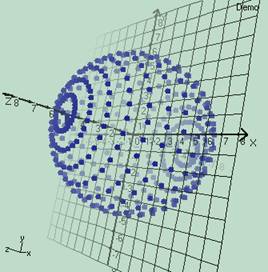
In the below you can see inside of this 3D sphere and another sphere that stays outside of this sphere. (But from this picture we can not understand whether this white sphere has a thickness or not.)

Now we let’s see striped view of the graph instead of the polygon view. (We notice that the white sphere does not have a thickness. So we say this sphere is 2 dimensional.)

      0<a<Pi    and a(step)=0.3

  Pi/5<b<2*Pi and b(step)=0.3

      4<r<5      and r(step)=1

fx(a,b,r) = r*sin(a)*cos(b)

fy(a,b,r) = r*cos(a)

fz(a,b,r) = r*sin(a)*sin(b)

You must notice another thing in this equation. Variants a, b and r in the equation are loop variants for 3DMath Explorer. Moving from this fact we can say ‘Dimension number of a curve that drawn with 3DMath Explorer are equal to number of variant that it has’ .

Lastly let’s examine dimension of basic elements point, line, plane and curve that exist in graph space

Point

   • Does not have a dimension (they are only coordinates),

   • Could be defined in all coordinate systems.

Line

   • has only one dimension,

   • require (need) a coordinate system (or a plane) that at least has two axis’s (or two dimension) to be drawn,

   • Has a length.

Plane

   • has two dimension,

   • requires (need) a coordinate system (or a plane) that at least has three axis’s (or two dimension) to be drawn. (Exception is the plane may be smooth and be just on the very same two-dimensional coordinate system. In fact two-dimensional coordinate systems also are planes may define as a two-dimensional curve and exist in a three dimensional coordinate system (in a graph space) or in itself, in a two-dimensional-plane coordinate system.)

   • Has surface area and might have surround/circle length.

Curve

   • May be 1,2,3 and 4 (and n) dimensional.

   • required (needed) axis number to be drawn change with their dimensions

   • If they are one dimensional have a length, if they are two dimensional have a surface aria and if they three dimensional have a volume.

As a human being and a subject like table and chair, we live in a 4 dimensional word. With a time dimension as a 4th dimension, we exist in this real coordinate system. But we are 3 dimensional objects just have a life and spend it in a 4 dimensional word.

Thank you for your interest and bother to read such a long article. If I manage to tell you something really interesting, that makes me happy.

I wish you a good life in this 4 dimensional word.

Written by Dursun TEBER, TEBER.biz, Ltd. (09.10.2002, Istanbul/Turkey)

dursun@teber.biz

http://www.teber.biz

This article is Copyright © 2002 byTEBER.biz, Ltd. All rights Reserved. Any reproduction or reuse of these pages or their contents requires the advance permission of Dursun TEBER of TEBER.biz, Ltd.

-3-