1. GRAFİK SİSTEMİ ve BOYUT KAVRAMI

1.3. Grafik Uzayında Nesnelerin Boyutları

Bu bilgilerden sonra grafik uzayında nesnelerin boyutları hakkında yazımıza geri dönelim.

Giriş olarak ‘Basit bir kürenin boyutu nedir?’ diye soralım. Eğer ‘3 boyutludur.’ diyenlerdenseniz bu yazıyı okumaya devam etmenizi tavsiye ederim. (Tabi bizde zorlama yok.)

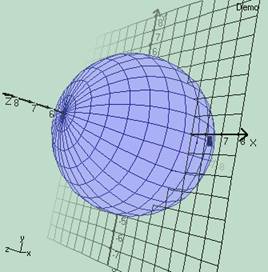
Aşağıda merkezi orjinde bulunan ve yarıçapı 5 olan bir kürenin (küre eğrisinin) matematiksel ifadesini görüyorsunuz.

  0<a<Pi

  0<b<2*Pi

fx(a,b) = 5*sin(a)*cos(b)

fy(a,b) = 5*cos(a)

fz(a,b) = 5*sin(a)*sin(b)

Şimdi bu eğrinyi Eğriçiz'de çizelim. a ve b örnekleme aralıkları pi/15 olarak seçerek isek, görüntü aşağıdaki gibi olacaktır.

  a(artış)=pi/15

  b(artış)=pi/15

Şimdi bu grafiklere bakarak hala kürenin 3 boyutlu olduğunu söyleyebilirsiniz. Evet bu eğrinin görüntüsü 3 boyutludur ve eğri 3 boyutlu bir koordinat sistemi içerisinde var olabilmektedir. Ancak eğri gerçekte 3 boyutlu mudur?

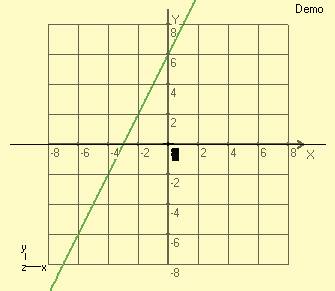
İsterseniz konuyu basitten karmaşığa doğru (yani tüme varım) ele alalım. Mesela basit bir fonksiyon eğrisini alalım. y=2*x+6 basit fonksiyon eğrisi XY düzlemi üzerinde yer alır. Yukarıdaki küre denklemine 3 boyutlu diyen arkadaşlar herhalde buna da ‘2 boyutludur’ diyecekler. Basit fonksiyon eğrilerinin görüntüsü 2 boyutlu bir koordinat sisteminde çizildiklerinde 2 boyutlu olur. Ancak bu eğriler 3 boyutlu koordinat sisteminde de çizilebilirler. Bu durumda görüntüsü 3 boyutlu olacaktır. Yani bu durumda da eğriye 3 boyutlu mu diyeceğiz?

Konuya devam etmeden önce bu örnek eğrimizi de EğriÇiz de şöyle bir inceleyelim. y=2*x+6 basit fonksiyon eğrisi üç boyutlu koordinat sisteminde ifadesi aşağıdaki gibidir

  -8<x<8

fx(x)= x

fy(x)= 2*x+6

fz(x)= 0

Bu eğrinin XZ Düzleminde çizilecek benzeri z =2*x+6 eğrisidir.

  -8<x<8

fx(x)= x

fy(x)= 0

fz(x)= 2*x+6

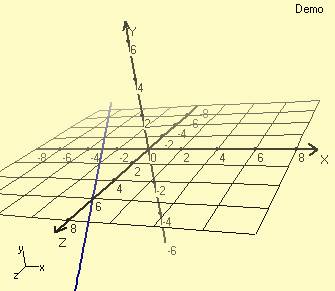
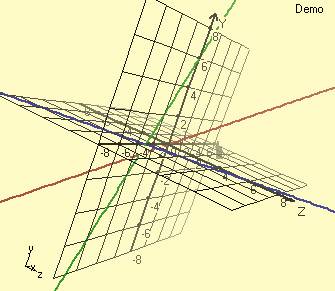
Tüm eksenler 45 derece (Pi/4) açı yapacak basit bir eğri denklemi ise,

  -8<m<8

fx(m) = m

fy(m) = m

fz(m) = m

Şeklinde tanımlanır. Şimdi tüm bu eğrileri bir arada görelim.

Bu arada isterseniz bu grafikte yardımcı çizim elemanları olarak kullandığımız XY ve XZ Düzlemlerinin de üç boyutlu koordinat sisteminde matematiksel ifadelerini de verelim.

XY Düzlemi:   -8<x<8   -8<y<8 fx(x,y) = x fy(x,y) = y fz(x,y) = 0

XZ Düzlemi:   -8<x<8   -8<z<8 fx(x,y) = x fy(x,y) = 0 fz(x,y) = z

YZ Düzlemi:   -8<y<8   -8<z<8 fx(y,z) = 0 fy(y,z) = y fz(y,z) = z

Konuya geri dönersek. Matematik de nesnelerin boyutları hakkında sormuş olduğum sorulara yanlış cevap verilmesinde yatan neden görüldüğü üzere nesnenin boyutunun çizildiği sistemin (koordinat sisteminin) boyutu ile karıştırılıyor olmasıdır.

Buraya kadar herhalde sorunu ortaya koyabildik. Pekala şimdi ‘Bir cismin boyutunun ne olduğunu nasıl söyleriz? Bunun için nasıl bir kısas (ölçü) kullanacağız?’ sorularına yanıt arayabiliriz.

Bu soruların cevabı cisimlerin uzunluk, yüzey alanı, hacim gibi özelliklerinde yatmaktadır. Matematik uzayında çisimler, bu özelliklere, boyutlarına bağlı olarak sahip olurlar veya olmazlar.

İsterseniz uzunluk, alan ve hacim kavramlarını şöyle bir inceleyelim. Düz bir çizginin boyu uzunluğudur. Bir dikdörtgen en(genişlik) ve boy olmak üzere iki uzunluğa sahiptir. Dikdörtgenin düzlemde sınırlamakta olduğu bir alan ve çevre uzunluğu vardır. Dikdörtgenler prizması eni (genişliği), boyu (uzunluğu) ve yüksekliği (derinliği) olmak üzere 3 uzunluğa sahiptir. Dikdörtgenler prizması uzayda bir hacmi sınırlar ve sahip olduğu 6 yüzeyin yüzey alanları vardır.

Boyutlarına bağlı olarak cisimlerin sahip oldukları özellikleri şöyle sıralayabiliriz.

Bir Boyutlu Cisimler

   • Uzunluğu vardır.

   • Çember, dikdörtgen gibi belli bir başlangıç ve bitiş noktası olmaması durumunda çevre uzunluğundan bahsedilir.

   • Yüzey alanı ve hacmi yoktur.

   • Gerçek hayatta var olamazlar. Yalnızca fikren veya düşüncenin kağıt ve ekrana yansımış görüntüleri olarak var olabilirler

İki Boyutlu Cisimler

   • Yüzey alanı vardır.

   • Çevre uzunluğundan ve en-boy kavramlarından söz edile bilinir.

   • Hacmi yoktur.

   • Gerçek hayatta var olamazlar

Üç Boyutlu Cisimler

   • Hacmi vardır.

   • En(genişlik), boy(uzunluk) ve yükseklik(derinlik,kalınlık) kavramlarından bahsedile bilinir.

   • Yüzey alanlarından söz edile bilinir.

   • Gerçek hayatta da var olabilirler.

Son maddeler dikkatinizi çekmiş olmalı. Gerçek hayat, zaman boyutu ile birlikte 4 boyutludur. Cisimler ‘Şu an’ adını verdiğimiz zaman kesitinde 3 boyutlu uzayda vardırlar. Bir cismin üç boyutlu gerçek uzayda var olabilmesi için bir hacme sahip olması gerekir. 1 ve 2 boyutlu cisimler bir hacme sahip olmadıkları için gerçek hayatta var olamazlar.

Buradan artık şu genellemeye gidebiliriz; yalnızca boyu olan çisimler 1 boyutlu, yüzey alanı bulunan ancak hacmi bulunmayan cisimler 2 boyutlu ve hacmi bulunan çisimler 3 boyutludur.

Bu genellemeden sonra kürenin boyutu ile ilgili sorumuza geri dönersek. Her ne kadar örnek küremizin grafikleri 3 boyutlu koordinat sisteminde çizilmiş olması nedeniyle 3 boyutlu grafikler olsa da bu küre gerçekte 2 boyutlu bir nesnedir. Çünkü kürenin bir yüzey alanı vardır ancak hacmi yoktur.

Şu anda, bu yazıyı yazarken bile bir sürü itiraz duyar gibi oluyorum. Mesela ‘Kürenin hacmi nasıl olmaz? Kürenin hacim formülü diye bir şey yok mu?’ diyebilirsiniz. Evet tabi ki kürenin bir hacim formülü var. Ancak bu formülden bahsedilirken ‘içi dolu kürenin hacmi’ ifadesi kullanılır.

Basit küre eğrisi, sahip olduğu yüzey ile uzayda bir hacmi sınırlar. Aslında yalnızca bir kabuktur. Kalınlığı (yüksekliği, derinliği) olmayan hiçbir cismin hacmi olamaz. Bu küre eğrisinin bir kalınlığı olmadığına göre hacmi de yoktur.

( Burada parantez içerisinde daha sonra birilerinin başımı ağrıtmaması için bir açıklama yapmam gerekiyor. Daha önce hacmi olmayan cisimlerin gerçek hayatta var olamayacağını söylemiştim. Yukarıdaki iki boyutlu kürenin hacmi olmadığını söylüyorum. Öyle ise bu küre de gerçek hayatta var olamaz. Var olmayan bir çisim nasıl olurda uzayda bir hacmi sınırlandırır? Evet iki boyutlu bu eğri gerçek uzay da var olamaz ve dolayısıyla gerçek uzayda hiç bir şeyi sınırlandıramaz. Ancak söz konusu matematik uzayı (grafik uzayı) olduğunda 1 ve 2 boyutlu çisimler bu uzayında var olurlar yani gerçektirler. Dolayısıyla çember veya dikdörtgen gibi 1 boyutlu çisimler bu uzayda bir alanı, yukarıdaki 2 boyutlu küre gibi çisimler de bir hacmi sınırlandırırlar. )

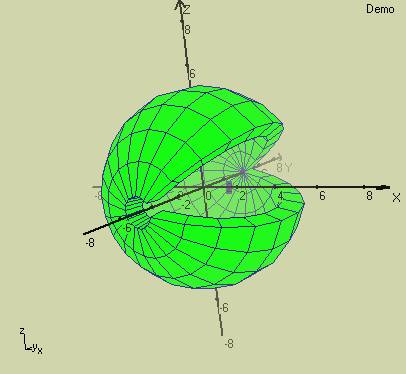
Yukarıdaki 2 boyutlu basit küre nesnesini 3 boyutlu yapmak için bir kalınlık boyutu vermeliyiz. Bunu da 5 olan yarıçapını değişken haline getirerek yapabiliriz.

      0<a<Pi    ve a(artış)=0.3

  Pi/5<b<2*Pi ve b(artış)=0.3

      4<r<5      ve r(artış)=1

fx(a,b,r) = r*sin(a)*cos(b)

fy(a,b,r) = r*cos(a)

fz(a,b,r) = r*sin(a)*sin(b)

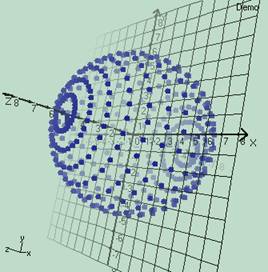
Aşağıda yukarıdaki 3 boyutlu kürenin içinden dışarıya doğru bakarak dışarısında yer alan başka küreyi görmekteyiz. (Bu görüntüde beyaz kürenin bir kalınlığının olup olmadığı anlaşılamıyor)

Aşağıda yukarıdaki görüntünün poligon ile kaplamak yerine çizgi ile çizilmiş halini görüyorsunuz. (Dıştaki kürenin bir kalınlığı olmadığı fark ediliyor. Öyle ise bu küre 2 boyutludur diyoruz.)

      0<a<Pi    ve a(artış)=0.3

  Pi/5<b<2*Pi  ve b(artış)=0.3

      4<r<5       ve r(artış)=1

fx(a,b,r) = r*sin(a)*cos(b)

fy(a,b,r) = r*cos(a)

fz(a,b,r) = r*sin(a)*sin(b)

denkleminde bir şeye daha dikkat etmiş olmalısınız. Denklemde yer alan a,b ve r değişkenleri EğriÇiz için birer döngü değişkenleridir. Bundan yola çıkarak EğriÇiz’de çizilen eğrilerin boyut sayısı döngü değişkenlerinin sayısı kadardır diyoruz.

Son olarak grafik uzayında var olan temel elemanlar yani nokta, çizgi, düzlem ve eğri’nin boyutlarını bir inceleyelim;

Nokta

   • Boyutu yoktur (yalnızca bir koordinattır.)

   • Tüm koordinat sistemlerinde tanımlanabilir

Çizgi

   • Tek boyutludur

   • Çizile bilinmesi için en az iki eksenli (iki boyutlu) bir koordinat sistemi (bir düzlem) olmalıdır

   • Uzunluğu vardır

Düzlem

   • İki boyutludur

   • Çizile bilmesi için en az üç eksenli bir koordinat sistemi (üç boyutlu grafik uzayı) olmalıdır.(istisnai durum: tanımlanan düzlemin, 2 boyutlu koordinat düzleminin kendisi olması durumudur.)

    • Yüzey alanı vardır. Çevre uzunluğundan söz edile bilinir.

Eğri

    • 1,2,3 ve 4 (ve de n) boyutlu olabilir.

    • Çizile bilmesi için gerekli eksen sayısı boyutuna bağlı olarak değişir

    • Tek boyutlu ise uzunluğu, iki boyutlu ise yüzey alanı, üç boyutlu ise hacmi vardır.

Written by Dursun TEBER, TEBER.biz, Ltd.

dursun@teber.biz

http://www.teber.biz

This article is Copyright © 2002 byTEBER.biz, Ltd. All rights Reserved. Any reproduction or reuse of these pages or their contents requires the advance permission of Dursun TEBER of TEBER.biz, Ltd.

-3-