| TEBER.biz | | Ana Sayfa | English | | |||||||
| >> EĞİTİM MATERYALLERİ | ||||||||
|
||||||||
2. Matematiksel Fonksiyonların Mantıksal Karşılıkları2.2. Mutlak Değer Fonksiyonunun (abs) Mantıksal KarşılığıMutlak değer fonksiyonu, ifadeyi negatif değerlerinden soyutlaya, ifadenin negatif değerlerini de pozitif yapan bir fonksiyondur. Klasik matematiksel ifadesi; | x - 2 | şeklinde iki düz çizgi içerisine ifadenin yazılması şeklindedir.
Bu fonksiyon bilgisayar ortamında abs adı ile isimlendirilmiş bir fonksiyon olarak karşımıza çıkar. Yukarıdaki ifade bilgisayara abs( x - 2 ) şeklinde girilir.
Mutlak değer fonksiyonu mantıksal olarak aşağıdaki söz diziminin görevini yerine getirir.
y = | x - 2 | ifadesini ele alalım. Bu ifade Bilgisayar ortamında;
y = abs( x - 2 ) şeklinde ifade edilecektir. Bu bilgisayar fonksiyonunun yaptığı iş koşul cümlesi ile aşağıdaki gibi yapılır
y = x - 2
if y < 0 then y =-y
Yukarıdaki koşulda ynin negatif bir sayı olması durumunda (negatif) olan işaretini yine ' (negatif) ile çarparak. İşaret çarpımının * = + özelliğinden faydalanıyoruz. y= -y yerine y = -1*y da diyebiliriz. (Ançak ilk ifade bilgisayar tarafından çok daha hızlı şekilde çözecektir.)
EğriÇiz de <, <=, >, >=, =, <>, lt, le, gt, ge, eq, ne mantıksal operatörleri ifadenin mantıksal doğru (true) olması durumunda 1, yanlış (false) olması durumunda 0 sayısal değerini döndürürler. Yani 5>2 mantıksal karşılaştırma 1 sayısal değerini döndürürken, 5>9 karşılaştırması 0 sayısal değerini döndürür.
Bundan faydalanarak yukarıdaki koşul cümlesini şöyle değiştirebiliriz.
y = x - 2
y = [(y >0) (y<0)] * y
[(y >0) (y<0)] ifadesi y<0 olması durumunda -1 değerini döndürerek negatif işaretli ynin işaretini -1 ile çarpmak sureti ile pozitif, y >0 olması durumunda ise 1 değerini döndürerek pozitif işaretli ynin işaretini 1 ile çarpmak sureti ile değişmemesini sağlar. (y=0 olması durumunda ise her iki koşulunda dışında kalınacağı için köşeli parantezden 0 değeri döndürülür. Bu durumda ise 0*0=0 dan 0 değeri korunmuş olunur.)
Şimdi bunları Eğriçiz de grafik üzerinde inceleyelim
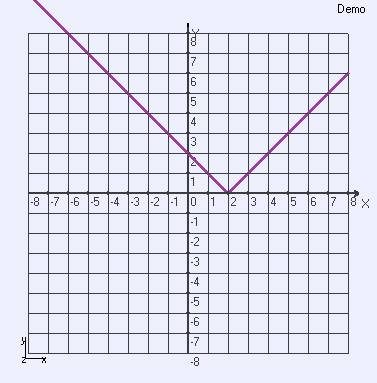
y = | x - 2 | birinci dereceden basit fonksiyon eğrisinin üç boyutlu koordinat sisteminde aşağıdaki gibi ifade edilmektedir. -8<x<8 fx(x) = x fy(x) = abs(x-2) fz(x) = 0
Biz abs fonksiyonunu kullanmadan, mantıksal operatörlerden faydalanarak bu eğriyi nasıl çizeriz sorusuna yanıt arıyoruz. Öyle ise bu denklemi şu şekilde değiştireceğiz. -8<x<8 fx(x) = x fy(x) = (y=x-2)*[(y>0) (y<0)] fz(x) = 0
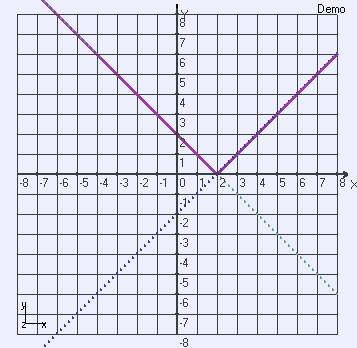
Aşağıda y>0 durumunda kullanılacak y= x-2 basit fonksiyon eğrisinin Eğriçizde çizmek için 3 boyutlu koordinat sistemi tanımını görüyorsunuz. -8<x<8 fx(x) = x fy(x) = x-2 fz(x) = 0
Aşağıda ise y<0 durumunda kullanılacak y=-(x-2) basit fonksiyon eğrisinin Eğriçizde çizmek için 3 boyutlu koordinat sistemi tanımını görüyorsunuz. -8<x<8 fx(x) = x fy(x) = -(x-2) fz(x) = 0
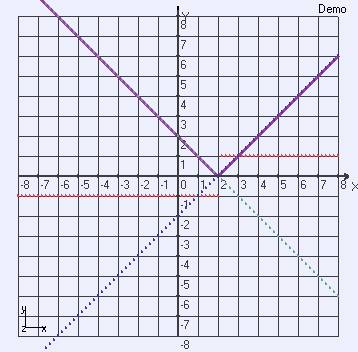
Şimdi tüm bu eğrileri aynı grafik üzerinde bir görelim. Aşağıda mantıksal mutlak değer eğrisinin çizgi ile diğer eğrileri ise ayrık noktalar halinde çizilmiş halini görmektesiniz.
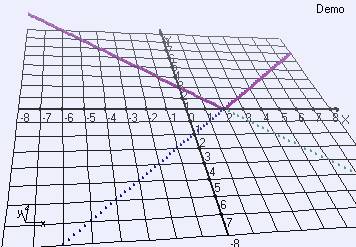
İsterseniz bu grafiği x ve y eksenlerinde -54 ve 14 derece döndürerek ortaya çıkan şekli de bir görelim.
Mutlak değer fonksiyonunun diğer bir ifadesi, değerin işaret fonksiyonundaki karşılığı ile çarpılmasıdır. Yani
abs(f(x))=f(x)*sgn(f(x))
İşaret fonksiyonunun mantıksal karşılığı ise
Sgn(f(x))= (f(x)>0) (f(x)<0)
(işaret fonksiyonu f(x)>0 ise 1, f(x)<0 ise -1 ve 0 ise 0 değerlerini alır.)
Şeklindedir. Buradan Abs fonksiyonunu mantıksal karşılığı
abs(f(x))= f(x)*[(f(x)>0) (f(x)<0)]
(abs fonksiyonu f(x)>0 ise f(x), f(x)<0 ise f(x) ve f(x)=0 ise 0 değerlerini alır.)
şeklinde ifade edile bilinir.
fy(x) = abs(x-2) = (x-2)* [((x-2)>0) - ((x-2)<0)] =(y=x-2)* [(y>0) - (y<0)]
Written by Dursun TEBER, TEBER.biz, Ltd. |
|
Questions or problems regarding this web site
should be directed to dursun@teber.biz
. Copyright © 2002 Dursun TEBER. All rights reserved. ( http://www.teber.biz ) Last modified: 15/06/2002. |